ベイズの定理はイギリスの牧師・数学者であったトーマス・ベイズが発見したといわれる定理です。最初にある確率(Prior Probabilities)がすでにあったとします、ベイズの定理はその後新しい情報が加わり、最初の確率 Prior Probabilities を訂正・更新するときに使われます。

どういうことかというと、
例えば、弁護士になるための司法試験は難関で合格率約 26％と言われています。１００人うけても２６人しか受からないような難易度と言えます。とりあえずここでは司法試験の合格率は 26％とします。つまり Prior Probability は 26%です。

弁護士になるため司法試験を受ける A 君と B 君がいます。

A 君は法学部卒です。
B 君は法学部卒ではありません。

果たして二人にとっては司法試験の合格率は 26％と同じでしょうか？

gokaku

ベイズの定理 P(H|E)=P(E|H)*P(H)/P(E)

最初の仮説を H、新しい条件の根拠を E とします。 H は仮説という意味の Hypothesis の頭文字から、E は根拠・証拠という意味の Evidence からとられています。

P(H):最初の仮説の確率
P(E):新しい条件の根拠の確率
P(E|H)：最初の仮定を条件とした、新しい根拠となる確率
P(H|E)=P(E|H)*P(H)/P(E)というのはベイズの定理によって導き出される修正後の確率です。

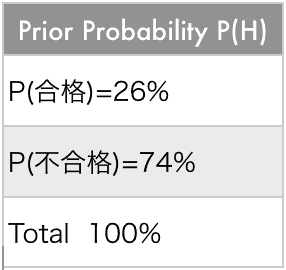
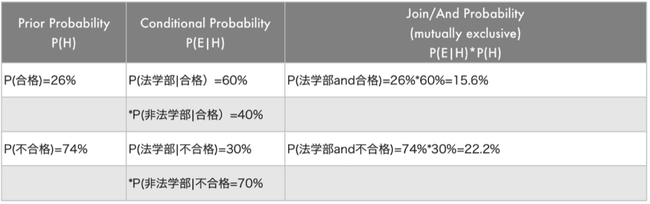
司法試験の例でみてみます。 P(H): P(合格)は 26%です。逆に合格の反対は不合格しかないので P(不合格)は 74%です。

P(H)の確率 P(合格): 合格の確率

先の例ので司法試験の合格率は 26%でした。
つまり Prior Probability は 26%です。

P(H): P(合格)は 26%です。では、不合格の確率はいくつでしょうか？
このように合格かかそうでないか二択となるようなものは、互いに重複するような条件でない・その二択以外のものはないというような関係であり MECE (Mutually Exclusive and Collectively Exhaustive)と言います。

そのような関係であるため、合格の反対は不合格しかないので P(不合格)は 74%です。100%-26%=74%

prior-probability

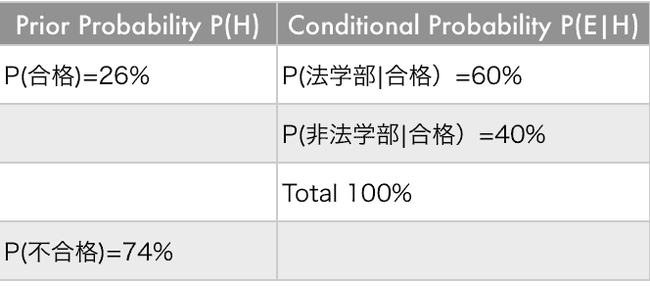
P(E|H)の確率 P(法学部|合格):合格者の中で法学部卒の確率

ここで合格した人に法学部卒であるか聞いた所 60%の人が法学部卒と答えました。逆に合格した人の中で法学部卒でない人は 40%です。100%-60%=40%

conditional-probability

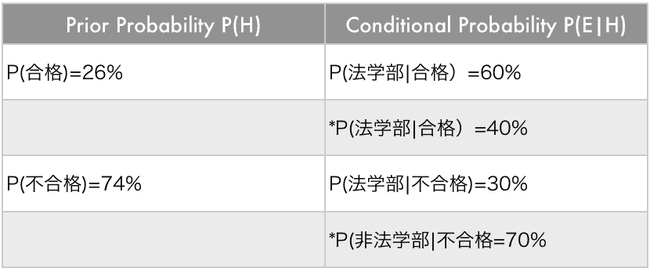
次に、不合格になった人にも法学部卒であるか聞いた所 30%の人だけが法学部卒と答えました。不合格した人の中で法学部卒の人は 70%です。100%-30%=70%

conditional-probability

P(E|H)*P(H)の確率 P(法学部 and 合格):（試験を受けた人の全体の中で）法学部かつ合格の確率

ここで前回のところで紹介した Multiplication Low of Probability 確率の掛け算の法則をつかって、

合格した人かつ法学部卒である場合
不合格した人かつ法学部卒である場合

の確率を計算してみると。 P(法学部 and 合格)は 15.6%で P(法学部 and 不合格)は 22.2%であることがわかりました。

conditional-probability

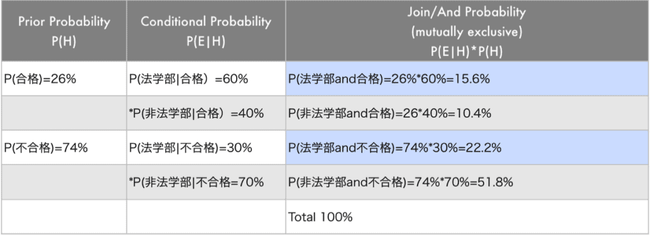
P(E)の確率 P(法学部):(試験を受けた人全体の中で)法学部である確率

他にも P(非法学部 and 合格)と P(非法学部|不合格)を求めます。そうすると合格不合格に関わらず法学部卒である確率 P(E)は 15.6%+22.2%で 37.8%であることがわかります。

conditional-probability

P(H|E)の確率：法学部の人が合格する確率

ここでベイズの定理 P(H|E)=P(E|H)*P(H)/P(E)の登場です。これまでに数値のわかった P(H)、P(E), P(E|H)をベイズの定理に当てはめると P(H|E)を求めることができます。

baye's-theorem-probability

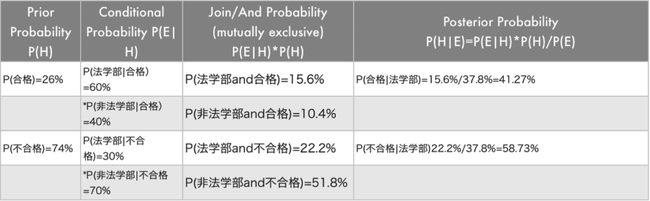
ベイズの定理を使った結果 P（合格|法学部)は 41.27%であることがわかりました。

最初の質問の答え

ここで最初の例の問題にもどってみます。

A 君は法学部卒です。
B 君は法学部卒ではありません。

果たして二人にとっては司法試験の合格率は 26％と同じでしょうか？
長くなりましたが答えは、法学部であるなら合格率は 41.27%であり。法学部卒の方が合格率が高いと言えることがわかりました。

BAYE’S THEOREM 　ベイズの定理の使われ方

ベイズの定理は保険の分野で使われたりします。
例えば、生命保険に入る時に家族に心臓病を患ったことがある人がいるかなど聞かれそれに応じて保険料が変わったりするのもベイズの定理を使い、P(H|E):P(心臓病| 家族に心臓病)を求めた結果、家族に心臓病を患ったことががある人がいる場合のほうが他の人よりも確率が高いからだと言えます。

このようにあるベイズの定理はある条件を追加していくことによりより正確な確率を修正していくことができます。

BASE RATE FALLACY 基準判断の誤謬

Baye’s からもう一つ学べる事は
P(H|E) は P(E|H)でないということです。

法学部だから司法試験に合格することは司法試験に受かったから法学部であるということは全く違うということです。言われて見れば当たり前のことです。

しかし、ときどき議論の場では混合されて話されることがみられます。「嘘つきは泥棒の始まり」なんてことわざがありますが。
泥棒であるから嘘つきであるのか嘘つきであるから泥棒であるのか、果たしてどちらでしょうか？

BAYE’S THEOREM の式