POISSON DISTRIBUTION ポアソン分布
Binomial Distribution では N 回の試行のうち何回 Success 成功するか見てきました。例えばコインを3回投げて2回表がでる確率は?など。
Poisson Distribution では特定の時間・距離・長さの間に何回成功するかを見ていきます。Poisson Distribution は以下のような確率を推測するのに適しています。
例1:時間のインターバル:ある特定の時間ごとにどのくらいの人が来るか?
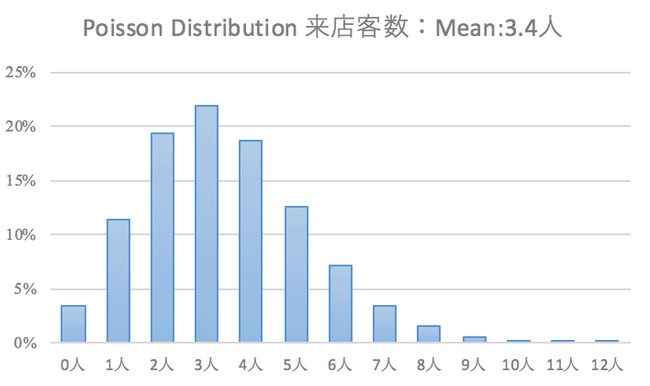
過去のデータから、日曜のランチタイム時1分間に平均 3.4 人(Mean)のお客さんが来ることがわかりました。その情報をもとに日曜のライチタイム時1分間に2人お客さんが来る確率を求めています。
Excel Function: Poisson Distribution =POISSON.DIST(x,mean,cumulative)
Excel の関数では POISSON.DIST を使い、求めたい成功の回数、Mean, 累積した確率かどうかを指定します。 2人ちょうどお客さんが来る確率は?
- X:求めたい成功の回数:2
- Mean:平均の数:3.4
- Cumulative:ちょうど二人来るときの確率なので 0
=POISSON.DIST(2,3.4,0)=約 19.29%
1 ~4人のお客さんが来る確率は?
Poisson Distribution を表にしてみます。 表ができたら 1 人~4人の確率のところを合計します。
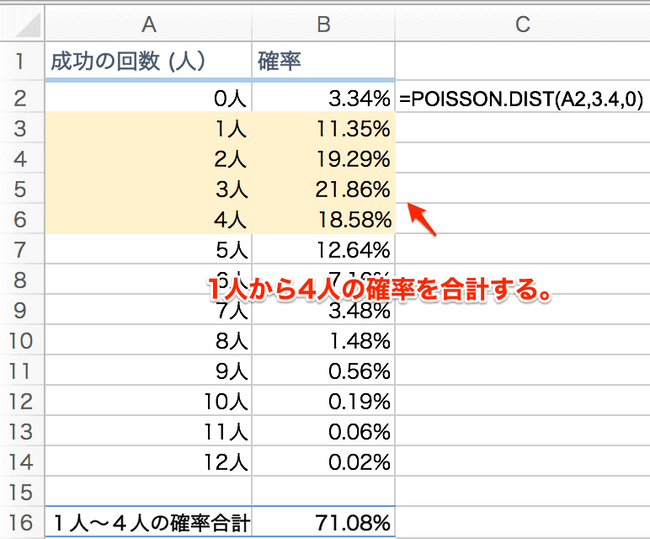
答えは約 71.08%です。
例2:距離のインターバル:ある特定の距離の間にどのくらいのある事おこるか?
過去のデータから、あるエリアにて電線の不具合が、100 km の間に平均で5回ある事がわかりました。
その情報をもとに、100km の間に 6 回以上不具合が起こる可能性を推測してみます。 Excel の関数=POISSON.DIST を使います。
- X:求めたい成功の回数: 6 回
- Mean:平均の数:5回
- Cumulative: ちょうど X 回のときは 0, X 回以下の時は 1 と入力すれば良いのですが、今回は6回以上です。
Excel の関数では”~以上”という指定はできないので一工夫必要になります。
まずは図表を作ってみます。
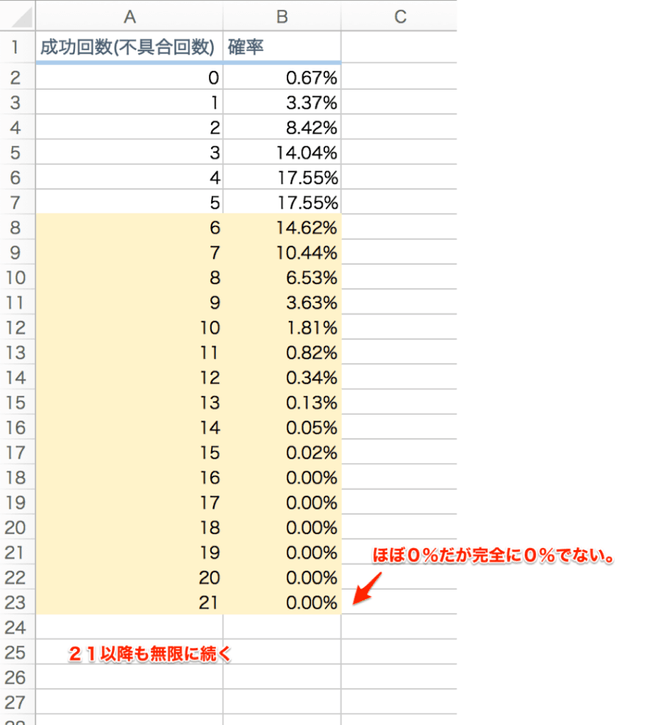
6回不具合の確率は約 14.62%で、7 回は約 10.44%、8 回は約 6.53%と次第に減っていきますが、厳密にいうと0%に達することはありません。
ただし、全部の確率を合計すると 100%になることはわかっています。
ではそのことを利用すると 100%から”5 回以下”のときの確率を引けばの 6 回以上の確率がわかるということです。
式で表すとこうなります。
6 回以上の確率=100% -POISSON.DIST (5,5,1)=約 38.4%
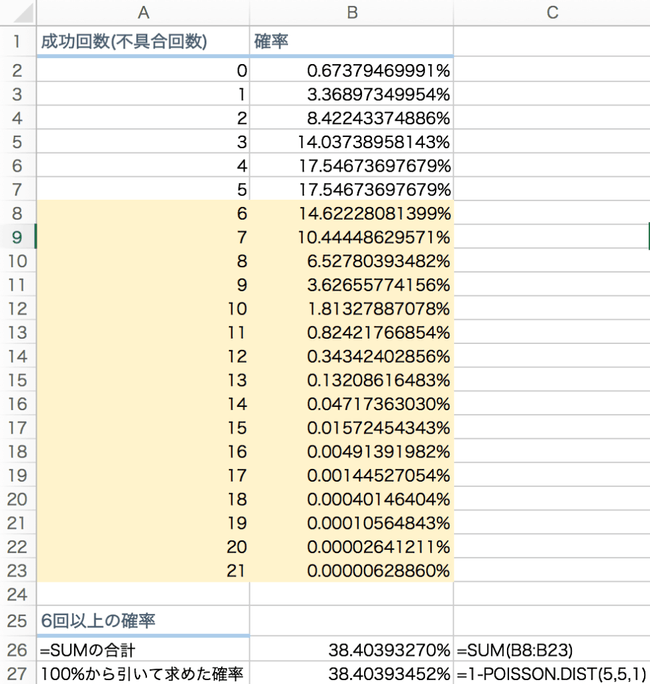
このように Excel の関数ではちょうど X 回もしくは X 回以下などでしか指定できないため。 今後も 100%(全体)から引く、大きい方から小さい方を引くなどの計算式の工夫はよく使われます。
POISSON EXPERIMENT の条件・特徴
Poisson Distribution は上記で紹介したような Poisson Experiment で使えます。ただし、Poisson Distribution であるためには Binomial Experiment でも確認したような条件があります。
1 成功の確率が一定のインターバルごとで同じであること。
例えば先の例で特定の距離の間では特に不具合が起こりやすいという場合は条件を満たしません。
2 成功の確率が他のインターバルの影響をうけない、独立した確率であること。
例えば、もしある区間 A で起きた不具合が原因で区間 B の不具合を誘発させるなどという場合は条件に満たしません。
3 成功の確率がインターバルのサイズに比例すること。
例えば先の例で、100km で平均5回であれば、200km では平均10回、300km では平均 15 回と比例していること。
4 Mean が Variance とほぼおなじ
Poisson Experiment では Mean と Variance がほぼおなじになります。
5 過去のデータより出した Relative Frequency Distribution が Poisson Distribution の形をしている。
過去のデータを使い Relative Frequency Distribution を作成したとき Poisson Distribution の形 Bell shape distribution に当てはまること。 過去に起きた実際のデータから作った Relative Frequency Distribution
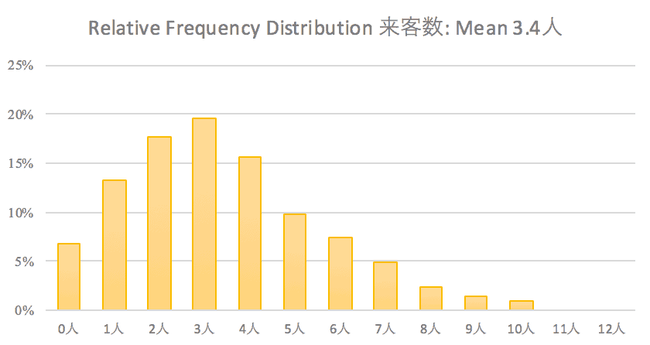
過去のデータを使い、Poisson Distribution にあてはめたときの図表 Discrete Random Variable= 1 分間に何人の来店があるか?